Výpočet inverzní matice a determinantu

Gauss-Jordanova eliminace vypočte přímo inverzní matici. U Gaussovy eliminace a LU dekompozice získáme inverzní matici řešením pro $n$ pravých stran, tvořených vektory standardní báze.

Všechny metody rovnocenné jak přesností, tak i počtem $n^3$ operací.

Determinant nepočítáme ze vzorců (růst zaokrouhlovací chyby), ale využijeme věty, že determinant součinu matic je roven součinu determinantů. Pro LU dekompozici

$$\det({\bf A}) = \det({\bf L}) \cdot \det({\bf U}) = \prod_{j=1}^n u_{jj}$$

Gaussova eliminace odpovídá násobení maticemi a pokud se sám řádek nenásobí a pouze se přičítají násobky jiných řádků, je determinant matice každé úpravy ${\bf D}_i = 1$ a determinant ${\bf A}$ se rovná součinu diagonálních prvků trojúhelníkové matice.

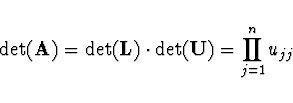
Pokud dochází k přehazování řádků při výběru hlavních prvků, dojde k násobení determinantu $-1$, je nutno si zapamatovat počet změn znaménka.