Speciální typy matic

Řídká matice má většinu prvků $= 0$.

Pro řešení soustav s řídkou maticí se často používají gradientní metody, spočívající v minimalizaci $\Vert {\bf A} \vec{x} - \vec{b} \Vert^2_{III}$. Pro řídkou matici je totiž počet operací pro výpočet ${\bf A} \vec{x} \sim n$, a ne $\sim n^2$ jako pro plnou matici.

Matice ${\bf A}$ je pásová, pokud $a_{ij} = 0$ pro $\vert i-j\vert > p.$ Tridiadonální matice pro $p = 1$, pětidiagonální matice pro $p = 2$.

Soustavy s tridiagonální maticí

$$\left( \begin{array}{cccccccc} a_1 & b_1 & 0 & 0 & \ldots & ... ... \\ f_2 \\ f_3 \\ \vdots \\ f_{n-1} \\ f_n \end{array} \right)$$

Tridiagonální zapíšeme do 3 vektorů $\vec{a}$, $\vec{b}$, $\vec{c}$. V praxi téměř vždy tridiagonální matice, u kterých výběr hlavního prvku není potřebný (silně regulární matice).

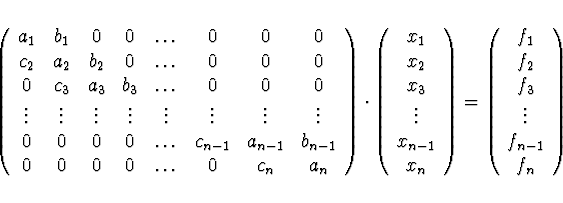
Řešení: Předpokládáme zpětný běh $x_k = \mu_k x_{k+1} + \rho_k$. Dosadíme

$$c_i \left( \mu_{i-1} x_i + \rho_{i-1} \right) + a_i x_i + b_i x_{i+1} = f_i$$

po úpravě

$$x_i = \frac{-b_i}{c_i \mu_{i-1} + a_i}\ x_{i+1} + \frac{f_i - c_i \rho_{i-1}}{c_i \mu_{i-1} + a_i}$$

výsledek

$$\mu_i = \frac{-b_i}{c_i \mu_{i-1} + a_i} \ \ \ \ \ \ \ \ \ \ \ \ \ \rho_i = \frac{f_i - c_i \rho_{i-1}}{c_i \mu_{i-1} + a_i}$$

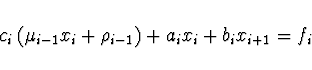
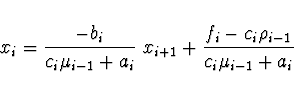
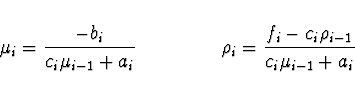
Startování $c_1 = 0, \ b_n = 0$ ( $\mu_0,\ \rho_0,\ x_{n+1}$) libovolné.

Blokově tridiagonální matice - ${\bf A}_i$, ${\bf B}_i$, ${\bf C}_i$ - malé matice $\Rightarrow$ ${\mu}_i, \ \rho_i$ - malé matice