Vnořené (embedded) Runge-Kutta metody

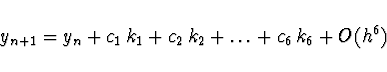
Těmto metodám se říká i Runge-Kutta-Fehlbergovy, jde o modernější přístup k adaptivní volbě integračního kroku.

Pro metody více než 4 řádu, musíme použít více přibližných vyjádření derivace než je řád metody. Například pro metodu 5. řádu je nutno sestavit kombinaci

$$y_{n+1} = y_n + c_1\, k_1 + c_2\, k_2 + \dots + c_6\, k_6 + O(h^6)$$

Lze ale zvolit taková $k_1$, $k_2$, ..., $k_6$, že z nich lze vytvořit i kombinaci, která dává metodu 4. řádu

$$y^{*}_{n+1} = y_n + c_1^{*}\, k_1 + c_2^{*}\, k_2 + \dots + c_6^{*}\, k_6 + O(h^5)$$

Tato formule se nazývá vnořená. Chybu metody můžeme odhadnout vztahem

$$\Delta \equiv y_{n+1} - y_{n+1}^{*} = \sum \limits_{i=1}^6 (c_i - c_i^{*}) k_i \ \ .$$

Použití vnořené formule podstatně zmenšuje počet nutných vyčíslení funkce $f(x,y)$.

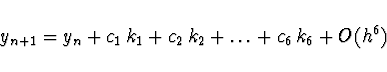
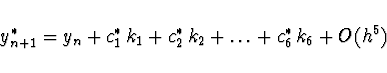
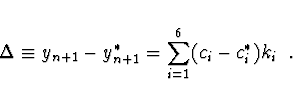
Spojité Runge-Kuttovy metody (dense output)

Aby byla Runge-Kuttova metoda efektivní, používáme velká $h$. Z různých důvodů, například pro vykreslení grafu, potřebujeme často znát hodnoty v mezilehlých bodech. Do čtvrtého řádu metody včetně lze hodnoty v mezilehlých bodech spočítat Hermiteovou interpolací z hodnot $y_i$, $y'_i = f(x_i, y_i)$, $y_{i+1}$ a $y'_{i+1} = f(x_{i+1}, y_{i+1})$.

Pro metody vyššího řádu používáme speciální metody pro spojité RK. Obvykle jsou k $s$ v metodě použitým $k_i$ přidány ještě další $k_i$, kde $i = s+1, \dots, s^{*}$, a rozdíl $s^{*} - s$ je roven dvěma nebo třem. Ty pak umožní, aby přesnost interpolace nebyla horší než přesnost integrace systému ODE.