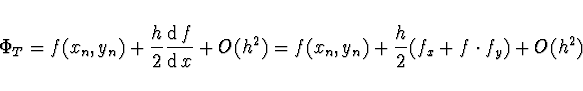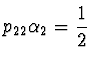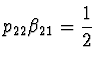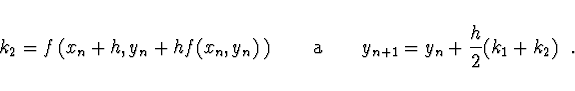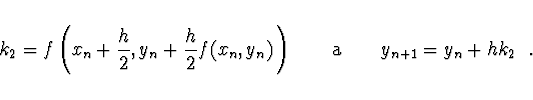

Next: Klasická Runge-Kuttova metoda čtvrtého
Up: Runge-Kuttovy metody pro řešení
Previous: Princip Runge-Kuttových metod
Zvolíme tedy 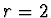 a můžeme odvodit
a můžeme odvodit
kde
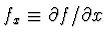 ,
,
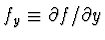 a
a 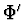 je derivace
je derivace 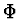 podle
podle 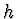 .
.
Porovnáme výrazy u nulté a první mocniny 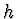 funkce
funkce 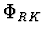 s přírůstkem
s přírůstkem 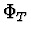 (
(
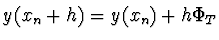 ) vyjádřeným
z Taylorova rozvoje
) vyjádřeným
z Taylorova rozvoje
a dostaneme
Tato soustava má nekonečně mnoho řešení, ale logice Runge-Kuttových
metod odpovídají následující 2 řešení
řešení.
- Řešení
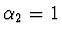 ,
,
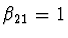 a
a
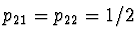 dává metodu analogickou lichoběžníkové metodě integrace.
Zde je
dává metodu analogickou lichoběžníkové metodě integrace.
Zde je
- Řešení
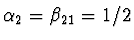 ,
, 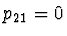 a
a
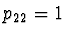 dává metodu analogickou obdélníkové metodě integrace.
Zde je
dává metodu analogickou obdélníkové metodě integrace.
Zde je


Next: Klasická Runge-Kuttova metoda čtvrtého
Up: Runge-Kuttovy metody pro řešení
Previous: Princip Runge-Kuttových metod
Jiri Limpouch
2000-05-25
![]() a můžeme odvodit
a můžeme odvodit
![]() funkce
funkce ![]() s přírůstkem
s přírůstkem ![]() (
(
![]() ) vyjádřeným
z Taylorova rozvoje
) vyjádřeným
z Taylorova rozvoje