Jsou to v praxi velmi často používané metody. K nalezení řešení
![]() se využívá pouze předchozího bodu
se využívá pouze předchozího bodu
![]() , nevyužívá bodů s indexem
, nevyužívá bodů s indexem ![]() . Takové metody
nazýváme jednokrokové.
. Takové metody
nazýváme jednokrokové.
Metody Runge-Kutta jsou založeny na postupném zpřesňování hodnot
v bodech mezi ![]() a
a ![]() včetně (obvykle se využívá bodu
včetně (obvykle se využívá bodu
![]() ). Výpočetní vzorec Runge-Kuttovy metody má tvar
). Výpočetní vzorec Runge-Kuttovy metody má tvar
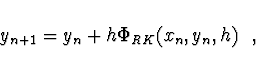
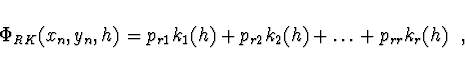
Pokud zvolíme ![]() , dostaneme Eulerovu metodu. Pro
, dostaneme Eulerovu metodu. Pro ![]() se řád
metody může rovnat
se řád
metody může rovnat ![]() (chyba 1 kroku
(chyba 1 kroku ![]() ). Pro konstrukci
metody 5. řádu je však zapotřebí alespoň
). Pro konstrukci
metody 5. řádu je však zapotřebí alespoň ![]() .
.