Metoda střelby

Máme $n_1$ podmínek v bodu $a$, $n_2$ podmínek v bodu $b$. Zkusmo zvolíme $n_2$ dodatečných podmínek v bodu $a$ a řešíme počáteční úlohu. Řešení v bodu $b$ dosadíme do $n_2$ původních podmínek, a podle výsledku měníme dodatečné podmínky v bodu $a$ tak, abychom se trefili do podmínek v bodu $b$. Musíme tedy řešit $n_2$ obecně nelineárních rovnic. Pokud je $n_2 = 1$, jde jen o 1 rovnici a úloha je podstatně snažší.

Název je vlastně od střelby na cíl, která je popsána 4 diferenciálními rovnicemi

$$\frac{{\rm d}\, x}{{\rm d}\, t} = v~\cos \theta \frac{{\rm d}\, v} {{\rm d}\, t} = - \frac{1}{2\, m} c \varrho s~v^2 - g \sin \theta$$

$$\frac{{\rm d}\, y}{{\rm d}\, t} = v~\sin \theta \frac{{\rm d}\, \theta} {{\rm d}\, t} = - \frac{g}{v} \cos \theta$$

a okrajovými podmínkami

$$x(0) = y(0) = 0 \quad v(0) = v_0 \quad y(x_c) = 0$$

Střelec volí náměr - úhel $\theta(0)$, tak aby zasáhl cíl. Pokud cíl mine opraví odhad $\theta(0)$ a zkouší to znovu. Musíme tedy řešit jednu nelineární rovnici pro $\theta_0 = \theta(0)$

$$y(x_c, \theta_0) = 0$$

Výpočet funkční hodnoty pro $\forall\, \theta_0$ vyžaduje řešení počátečního problému pro obyčejné diferenciální rovnice.

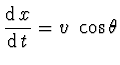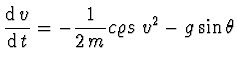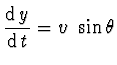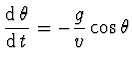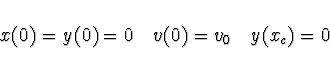
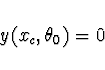
Pozn. Pokud je nutno řešit více nelineárních rovnic, používá se Newton-Raphsonova metoda, kde se parciální derivace počítají numericky.