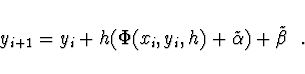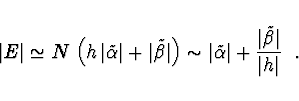Vlastnosti Runge-Kuttových metod

Runge-Kuttovy metody jsou velmi robustní - fungují téměř vždy, jsou velmi odolné k vlastnostem funkce $f$ (absence derivace, příp. skoky). Jsou to samostartující metody (není třeba na začátku použít jiné metody). Jsou jednoduché a dostupné v numerických knihovnách. Hodí se zvlášť, pokud není vyžadována vysoká přesnost.

Nevýhodou je relativně vysoký počet výpočtů funkce $f$ na jeden krok (při složitém výpočtu $f$ je metoda pomalá). Nehodí se pro řešení tzv. stiff rovnic (rovnic se "silným tlumením").

Nespojitost funkce $f$

Funkce $f$ je často nespojitá nebo má nespojité derivace. Například

$$y' = \left\{ \begin{array}{ll} f_{I} (x, y) & {\rm pro} \ g(... ...\\ f_{II} (x, y) & {\rm pro} \ g(x, y) < 0 \end{array}\right.$$

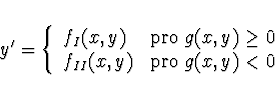
Možné strategie řešení tohoto problému:

1. Ignorujeme nespojitost a doufáme, že si nastavení kroku poradí samo.
2. Použijeme tzv. singularity detecting codes.
3. Hledáme bod nespojitosti a restartujeme výpočet od tohoto bodu metodu. Postup obvykle zmenší chybou i počet kroků.

Některé obecnější pojmy

O libovolné jednokrokové metodě, pro kterou platí vztah $y_{i+1} = y_i + h \Phi (x_i, y_i, h)$, říkáme, že je konzistentní, pokud

$$\lim \limits_{h \to 0} \Phi (x, y, h) = f(x, y) \quad {\rm pro} \quad \forall (x, y)\ \ .$$

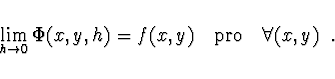
Metoda je regulární, pokud existuje konstanta $L$, $(x, y) \in G$, $(x, \tilde{y}) \in G$ a $h \in \langle 0, H \rangle$ tak, že platí

$$\vert\Phi (x, y, h) - \Phi (x, \tilde{y}, h)\vert \leq L \vert y - \tilde{y}\vert\ \ \ .$$

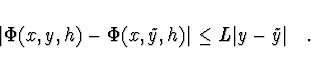
Věta Každá jednokroková regulární a konzistentní metoda je konvergentní.

Vliv zaokrouhlovacích chyb

Katastrofické případy - Příliš malý krok $x_i + h = x_i$ v $x$. Příliš malý krok se může projevit i v $y$, které zůstane $y_i + (y_{i+1} - y_i) = y_i$ konstantní po mnoha krocích, ač bez zaokrouhlování může být změna $y$ nezanedbatelná.

Kumulace chyb - Označme $\tilde{\alpha}$ chybu výpočtu $\Phi$ a chybu při přičtení změny $y(x,y)$ označme $\tilde{\beta}$. Pak tedy

$$y_{i+1} = y_i + h(\Phi(x_i, y_i, h) + \tilde{\alpha}) + \tilde{\beta}\ \ .$$

Pokud provedeme $N$ kroků o velikosti $N \sim \frac{1}{h}$, dosáhneme nejvýše (pokud mají všechny chyby stejné znaménko) celkové chyby

$$\vert E\vert \simeq N\, \left(h\, \vert\tilde{\alpha}\vert +... ...lpha}\vert + \frac{\vert\tilde{\beta}\vert}{\vert h\vert}\ \ .$$

Zaokrouhlovací chyby tedy rostou při zmenšování kroku $h$. Na druhé straně chyba metody roste při zvětšování $h$. Existuje tedy optimální krok $h$ z hlediska přesnosti.