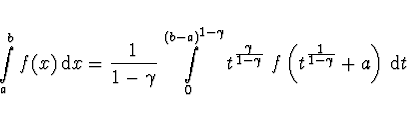Pozn. Neexistující nebo nekonečný integrál neřešíme, protože je to nekorektní úloha.
1. případ - funkci nelze počítat na okraji
Použijeme složené obdélníkové pravidlo
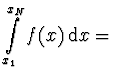 |
![$\displaystyle \left[ f_{\frac{3}{2}} +
f_{\frac{5}{2}} + \dots + f_{n - \frac{1}{2}} \right] +$](img57.gif) |
||
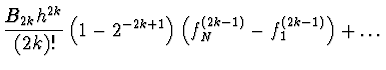 |
Při půlení podintervalů nelze využít předchozí body. Proto
užijeme ![]() , pak je implementace obdobná jako u lichoběžníkového
pravidla. I zde můžeme použít
Rombergovu metodu, která provádí extrapolaci integrálu na
, pak je implementace obdobná jako u lichoběžníkového
pravidla. I zde můžeme použít
Rombergovu metodu, která provádí extrapolaci integrálu na ![]() .
.
Integrál s nekonečnými mezemi
Integrál transformujeme na integrál s konečnými mezemi a pro ten
užijeme složené obdélníkové pravidlo.
Například po substituci ![]() dostaneme
dostaneme
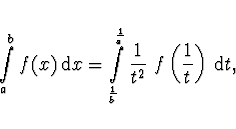
Často integrály rozdělíme
![]() tak, aby od bodu
tak, aby od bodu ![]() integrovaná funkce v absolutní
hodnotě klesala.
integrovaná funkce v absolutní
hodnotě klesala.
Integrál s integrabilní singularitou
Transformace záleží na charakteru funkce. Pokud
![]() , kde
, kde
![]() , provádíme transformaci
, provádíme transformaci
![]() . Potom
platí
. Potom
platí