Součtu těchto integrálů se říká složený vzorec.
K výpočtu integrálu přes zadaný interval není vhodné při rovnoměrné
síti použít vzorec jeden mnohabodový vzorec, přesný pro polynomy
až do vysokého stupně. Lepší je rozdělit interval do mnoha krátkých
podintervalů a v ![]() použít vzorec relativně nízkého řádu.
použít vzorec relativně nízkého řádu.
Součtu těchto integrálů se říká složený vzorec.
Složené lichoběžníkové pravidlo
![\begin{displaymath}
\int \limits_{x_1}^{x_N} f(x)\, {\rm d}x = h \left[ \frac{1}...
...ac{1}{2} f_N \right] + O\left(
\frac{(b-a)^3 f''}{N^2} \right)
\end{displaymath}](img22.gif)
Složené Simpsonovo pravidlo
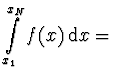 |
![$\displaystyle \left[ \frac{1}{3} f_1 +
\frac{4}{3} f_2 + \frac{2}{3} f_3 + \fra...
...t.
+ \left. \frac{2}{3} f_{N-2} + \frac{4}{3} f_{N-1} + \frac{1}{3} f_N \right]$](img25.gif) |
||
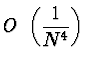 |
Ve střídání koeficientů není žádné magie, je to spíše nevýhodou.
Rozšířené Simpsonovo pravidlo ale lépe aproximuje okraje
než lichoběžníkové pravidlo. Vzorec 4. řádu přesnosti k konstantními
koeficienty uprostřed intervalu lze získat následovně.
Alternativa
![]()
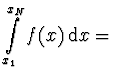 |
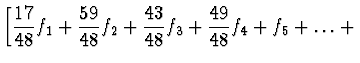 |
||
![$\displaystyle \left. \frac{49}{48} f_{N-3} \frac{43}{48} f_{N-2} +
\frac{59}{48} f_{N-1} + \frac{17}{48} f_N \right] + O~\left( \frac{1}{N^4}
\right)$](img29.gif) |