Metody, užívající sečnu

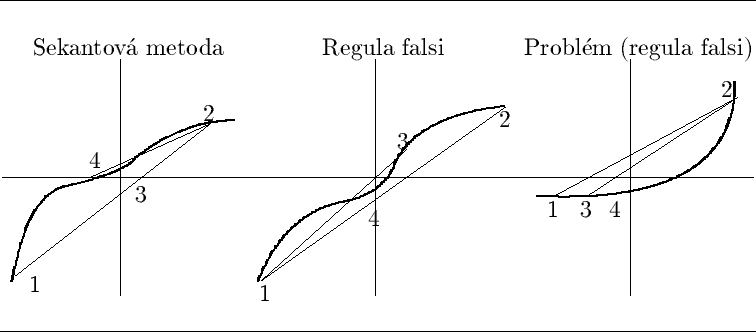
Sekantová metoda, metoda regula falsi a problém pomalé konvergence

Jsou-li body $a_{n-1}$ a $a_n$, pak bod $a_{n+1}$ zvolíme v průsečíku spojnice bodů $(a_{n-1},y(a_{n-1}))$ a $(a_n,y(a_n))$ s osou $x$.

Sekantová metoda - body $a_n$, $a_{n+1} \rightarrow$ bod $a_{n+2}$.
Ohraničení kořene nemusí být zachováno $\Rightarrow$ konvergence není zaručena!
V blízkosti kořene rychlejší než regula falsi. Pro rychlost konvergence platí $\lim \limits_{k \to \infty} \vert\epsilon_{k+1}\vert = C \vert\epsilon_k\vert^{1.618}$.

Metoda regula falsi - Po určení $a_{n+1}$ si k němu vyberu z z $a_{n-1}$ a $a_n$ bod $\tilde{a_n}$ tak, aby kořen zůstal ohraničen $f (a_{n+1}) \cdot f (a_n) < 1$. Konvergence je tudíž zaručena.
Metoda pomalejší než sekantová, ale je superlineární ($m > 1$).

Problém superlineárních metod - možnost velmi pomalé konvergence (malých kroků) daleko od kořene (viz obr).