Müllerova metoda hledání kořene

V bodech $x_i$, $x_{i-1}$ a $x_{i-2}$ budeme interpolovat zadaný polynom polynomem kvadratickým. Definujeme

$$t = \frac{x - x_i}{x_i - x_{i-1}} \ \ .$$

Funkci $f(x)$ interpoluje $\tilde f = A\, t^2 + B\, t + C$. Při hledání kořene této kvadratické rovnice substituujeme $u = 1/t$ a dostaneme $A + B\, u + C\, u^2 = 0$ s kořeny

$$u_{1,2} = \frac{-B \pm \sqrt{B^2 - 4\, A\, C}}{2C}$$

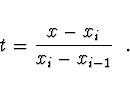
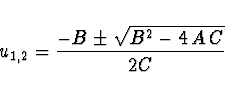
Odtud iterační vztah pro hledání kořene polynomu ve tvaru

$$x_{i+1} = x_i - (x_i - x_{i-1}) \left[ \frac{2C}{B \pm \sqrt{B^2 - 4AC}} \right],$$

kde $\pm$ nahradíme znaménkem $+$ nebo $-$ tak, aby byla maximální absolutní hodnota jmenovatele.

Pokud definujeme $q \equiv \frac{x_i - x_{i-1}}{x_{i-1} - x_{i-2}}$, můžeme koeficienty $A$, $B$ a $C$ zapsat ve tvaru

$$A \equiv q\, P(x_i) - q\, (1 + q)\, P(x_{i-1}) + q^2\, P(x_{i-2}),$$

$$B \equiv (2q + 1)\, P(x_i) - (1 + q)^2\, P(x_{i-1}) + q^2\, P(x_{i-2}),$$

$$C \equiv (1+q)\, P(x_i).$$

Pozn. I při hledání reálných kořenů můžeme při využití této metody dostat komplexní mezivýsledky.

Pozn. Používá se i pro komplexní kořeny analytických funkcí.