Řeším soustavu rovnic
![]() .
V prvním kroku nechť prvek
.
V prvním kroku nechť prvek ![]() (lze vždy dosáhnout přehozením
rovnic). Prvek
(lze vždy dosáhnout přehozením
rovnic). Prvek ![]() , použitý k úpravě rovnic 2, ..., n
nazveme hlavním prvkem (pivot).
, použitý k úpravě rovnic 2, ..., n
nazveme hlavním prvkem (pivot).
Od i-té rovnice odečteme 1.rovnici násobenou multiplikátorem
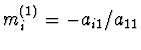 . Modifikovaná soustava bude mít v 1.sloupci
pod diagonálou samé 0. Úprava prováděná současně s pravou stranou
odpovídá násobení rovnice maticí
. Modifikovaná soustava bude mít v 1.sloupci
pod diagonálou samé 0. Úprava prováděná současně s pravou stranou
odpovídá násobení rovnice maticí
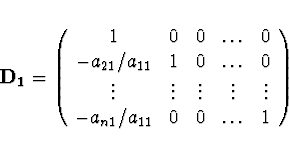
Po ![]() úpravách má matice
úpravách má matice
![]() tvar
tvar
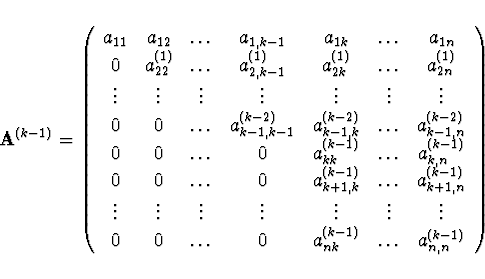
Pokud
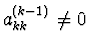 , lze ho zvolit za hlavní prvek,
spočítat multiplikátory
, lze ho zvolit za hlavní prvek,
spočítat multiplikátory
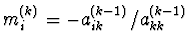 pro
pro
![]() a upravit příslušné rovnice.
a upravit příslušné rovnice.
V ![]() -tém kroku úpravy používám jako hlavní prvek prvek
-tém kroku úpravy používám jako hlavní prvek prvek ![]() -krát
upravený (odečítání!) hlavní prvek
-krát
upravený (odečítání!) hlavní prvek ![]() ztráta přesnosti
ztráta přesnosti
![]() výběr hlavního prvku.
výběr hlavního prvku.
Bez výběru hlavního prvku - přímé metody nepoužitelné pro obecné matice!!
Počet operací
Na každou 0
![]() vnitřních cyklů, potřebuji
vnitřních cyklů, potřebuji ![]() prvků
prvků ![]() 0. Celkový počet vnitřních cyklů
0. Celkový počet vnitřních cyklů ![]() (přesněji
(přesněji
![]() ), složitost algoritmu je řádu
), složitost algoritmu je řádu ![]() .
.
Gauss-Jordanova eliminace
Upravují se všechny prvky mimo diagonálu. Matice se převede na jednotkovou
![]() . Přímo spočtu inverzní matici
. Přímo spočtu inverzní matici ![]() . Vyšší počet
operací
. Vyšší počet
operací ![]() vnitřních cyklů.
vnitřních cyklů.