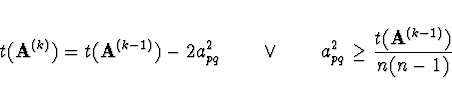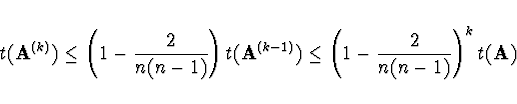Jacobiho transformace (metoda)

Jacobiho metoda nalezne $\forall$ vlastní čísla a vektory symetrické matice. Cílem je postupně zmenšovat čísla mimo diagonálu.

V každém kroku nalezneme v absolutní hodnotě maximální číslo mimo diagonálu $\vert a_{pq}\vert = \max \limits_{i,j < i} \vert a_{ij}\vert$. Pootočíme osy $p$, $q$ tak, aby se matice $\left[ a_{pp}\ a_{pq};\ a_{qp}\ a_{qq} \right]$ transformovala na diagonální.

Jeden ($k$-tý) krok iterace Jacobiho metodou má tvar

$${\bf A}^{(k)} = {\bf T}^{\rm T}_{p,q} {\bf A}^{(k-1)} {\bf T... ...& & & & \ddots & \\ 0 & & & & & & 1 \\ \end{array} \right] .$$

V této matici platí $c = \cos \varphi$ a $s = \sin \varphi$. Po $k$-té iterace je prvek matice

$$a^{(k)}_{pq} = (c^2 - s^2) a^{(k-1)}_{pq} - cs (a^{(k-1)}_{pp} -a^{(k-1)}_{qq})$$

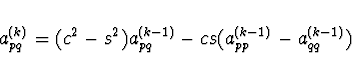
Aby se prvek $a^{(k)}_{pq} = 0$, úhel $\varphi$ musí splňovat vztah

$${\rm tg} 2 \varphi = \frac{2a_{pq}}{a_{pp} - a_{qq}}$$

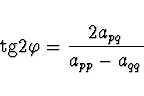
Důkaz konvergence Při posloupnosti Jacobiho transformací nejsou 0 mimo diagonálu trvalé. Důkaz konvergence je založen na konvergenci sumy mimodiagonálních prvků k 0.
Označme 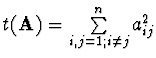$t({\bf A}) = \sum \limits_{i,j=1;i \not= j}^n a_{ij}^2$. Pak

$$t({\bf A}^{(k)})=t({\bf A}^{(k-1)}) - 2 a_{pq}^2 \qquad \vee \qquad a_{pq}^2 \geq \frac{t({\bf A}^{(k-1)})}{n(n-1)}$$

Tedy

$$t({\bf A}^{(k)}) \leq \left( 1 - \frac{2}{n(n-1)} \right) t(... ...k-1)}) \leq \left( 1 - \frac{2}{n(n-1)} \right)^{k} t({\bf A})$$

Posloupnost je tedy shora odhadnuta geometrickou posloupnosti s kvocientem $< 1$.