Nechť pro číslo
![]() takový,
že
takový,
že
![]() . Pak
. Pak ![]() je
vlastní číslo a vektor
je
vlastní číslo a vektor ![]() je vlastní vektor matice
je vlastní vektor matice ![]() .
.
2 typy úloh
Charakteristický polynom matice ![]() - determinant
- determinant
![]() .
.
Pozn. Je-li ![]() matice
matice ![]() , je charakteristický
polynom
, je charakteristický
polynom ![]() -tého stupně, a tedy má
-tého stupně, a tedy má ![]() kořenů (mohou být i vícenásobné). Ke
každému vlastnímu číslu
kořenů (mohou být i vícenásobné). Ke
každému vlastnímu číslu ![]() alespoň 1 vlastní vektor.
Počet
alespoň 1 vlastní vektor.
Počet ![]() lineárně nezávislých (LN) vlastních vektorů je
lineárně nezávislých (LN) vlastních vektorů je ![]() (
(![]() je násobnost vlastního čísla).
je násobnost vlastního čísla).
Pozn. Matice defektní má ![]() lineárně nezávislých
vlastních vektorů. Příklad
lineárně nezávislých
vlastních vektorů. Příklad
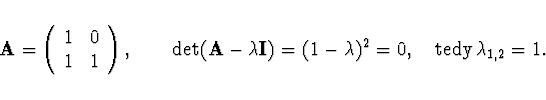
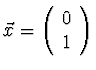 je jediným vlastním vektorem
je jediným vlastním vektorem
Pozn. Reálná matice může mít komplexně sdružená vlastní čísla
a vlastní vektory. Například
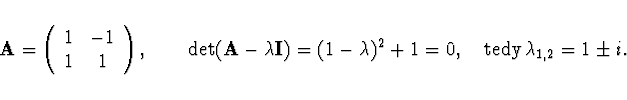
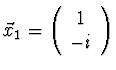 a
a
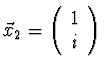 .
.
Normální matice ![]() je taková, že
je taková, že
![]() Normální matice řádu
Normální matice řádu ![]() má
má ![]() LN vlastních vektorů.
LN vlastních vektorů.
Pozn. Symetrická matice (
![]() ) má všechna vlastní čísla reálná.
) má všechna vlastní čísla reálná.
Pozn. Trojúhelníkové matice mají všechna
vlastní čísla na diagonále.
Věta Podobné matice ![]() a
a
![]() mají stejná vlastní čísla (stejné spektrum).
mají stejná vlastní čísla (stejné spektrum).
Odvození
Věta Ke každá matici ![]() jí podobná matice
v Jordanově normálním tvaru
jí podobná matice
v Jordanově normálním tvaru
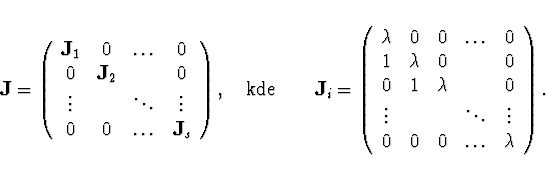
Pozn. Pro ![]() normální matici
normální matici ![]() podobná
matice diagonální.
podobná
matice diagonální.
Pozn. Neexistuje finitní postup jak provést transformaci matice
na Jordanův normální tvar.
Numerické metody řešení úplného problému vlastních čísel