

Next: Gradientní metody
Up: Přímé metody řešení soustav
Previous: Úlohy se žádným řešením
- Gauss-Jordanova eliminace
Při výpočtu se provádí 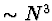 vnitřních cyklů (v každém cyklu jedno
násobení a jedno sčítání)
vnitřních cyklů (v každém cyklu jedno
násobení a jedno sčítání)
- Gaussova eliminace a LU dekompozice
Přímý běh je podstatně náročnější na počet operací.
U obou metod je k výpočtu přímého běhu potřeba
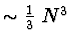 vnitřních
cyklů. Při zpětném běhu
vnitřních
cyklů. Při zpětném běhu
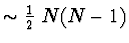 v Gaussově eliminaci.
Při LU dekompozici jsou zapotřebí 2 zpětně běhy, ale přímý běh je nepatrně
kratší, protože se neupravuje pravá strana, operací je u Gaussovy eliminace
i LU dekompozice stejně. Pro výpočet inverzní matice jsou pracnosti
Gauss-Jordanovy eliminace, Gaussovy eliminace i LU dekompozice stejné.
v Gaussově eliminaci.
Při LU dekompozici jsou zapotřebí 2 zpětně běhy, ale přímý běh je nepatrně
kratší, protože se neupravuje pravá strana, operací je u Gaussovy eliminace
i LU dekompozice stejně. Pro výpočet inverzní matice jsou pracnosti
Gauss-Jordanovy eliminace, Gaussovy eliminace i LU dekompozice stejné.
- Metoda řádu
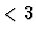 .
.
Byla dokázána (Strassen) existence metody, kde počet operací
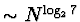 (
(
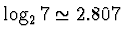 ) a tedy
roste s dimenzí
) a tedy
roste s dimenzí 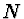 matice pomaleji než u klasických
metod, kde počet operací
matice pomaleji než u klasických
metod, kde počet operací 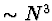 ,
Tato metoda vyžaduje komplikovanou průběžnou
archivaci napočítaných hodnot.
Pro malé matice je tato metoda podstatně pomalejší než
klasické metody a její výhody se projeví až matice řádu
,
Tato metoda vyžaduje komplikovanou průběžnou
archivaci napočítaných hodnot.
Pro malé matice je tato metoda podstatně pomalejší než
klasické metody a její výhody se projeví až matice řádu
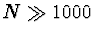 .
.


Next: Gradientní metody
Up: Přímé metody řešení soustav
Previous: Úlohy se žádným řešením
Jiri Limpouch
2000-03-08