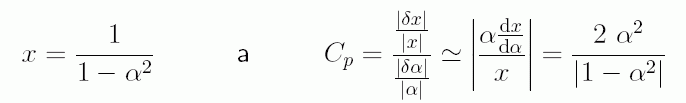Korektnost a podmíněnost úlohy

Korektnost úlohy

Definice: Nechť úlohou je najít řešení $\vec{y}\ \epsilon$ N (N je množina možných řešení) pro zadaný vektor $\vec{x} \epsilon$ M (M je množina vstupních dat). Pak úloha je korektní právě tehdy, jsou-li zároveň splněny obě následující podmínky

1.

$\exists$ právě jedno řešení $\vec{y}$ pro $\forall \ \vec{x} \epsilon$ M.

2.

Řešení spojitě závisí na vstupních datech, tj. jestliže pro $\forall n$ z množiny přirozených čísel je $\vec{y}_n$ řešení pro vstupní data $\vec{x}_n$, a jestliže $\vec{y}$ je řešení pro vstupní data $\vec{x}$, nechť dále $\rho$ je norma v množině vstupních dat a $\sigma$ je norma v množině možných řešení, pak platí

$$x_n \stackrel{\rho}{\rightarrow} x \ \Rightarrow \ y_n \stackrel{\sigma}{\rightarrow} y$$

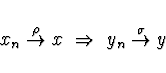
V praxi se řeší i nekorektní úlohy, ale 1. krok řešení spočívá v nalezení vhodného způsobu, jak převést úlohu na úlohu korektní (např. podmínkou na výsledek; interpretací vstupních dat; vhodnou volbou normy v prostoru řešení apod.)

Podmíněnost úlohy

Definice: Podmíněnost úlohy C_p  je daná poměrem relativní změny výsledku ku relativní změně vstupních dat, tj.

$$C_p = \frac{\frac{\Vert \delta y \Vert}{\Vert y \Vert}}{\frac... ... \delta x \Vert}{\Vert x \Vert}} \ \approx \ \frac{r(y)}{r(x)}$$

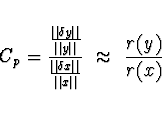
Pokud $C_p \sim 1$, říkáme, že úloha je dobře podmíněná, pokud C_p > 100, úloha je špatně podmíněná.
Pokud je přesnost použitého typu čísel $\varepsilon$ ( $r(x) = \varepsilon$) , pak úloha s $C_p > \varepsilon^{-1}$ není v rámci dané přesnosti řešitelná.
Často se pro špatně podmíněné úlohy používají speciální metody, které omezují růst chyb v průběhu výpočtu.

Příklad: Soustava lineárních rovnic s maticí blízkou k singulární (špatně podmíněná matice). Nechť je dána úloha

$$x + \alpha\ y = 1$$

$$\alpha\ x + y = 0$$

Nechť vstupem je hodnota $\alpha$ a výstupem hodnota x. Pak

$$x = \frac{1}{1 - \alpha^2} \ \ \ \ \ \ \ \ {\rm a} \ \ \ \ \ ... ...}{x} \right\vert = \frac{2\ \alpha^2}{\vert 1 - \alpha^2\vert}$$

Při $\alpha^2 \rightarrow 1$ je úloha špatně podmíněná.