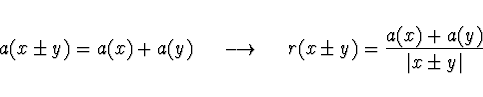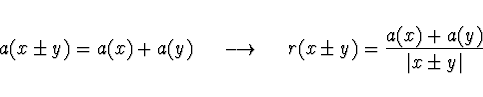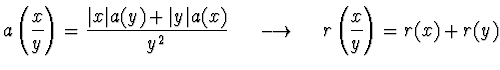

Next: Závislost charakteru chyby na délce kroku
Up: Zaokrouhlovací chyby
Previous: Reprezentace čísla v počítači
Nebezpečné jsou operace, které mohou podstatně zvětšit relativní chybu !!
Pokud výsledek malý
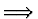 zvětší se silně
zvětší se silně
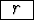 !!
Často nemohu rozhodnout, zda výsledek je 0 nebo není !!
!!
Často nemohu rozhodnout, zda výsledek je 0 nebo není !!
Odečteme-li např. čísla 1.32483726, 1.32483357 známá na 9 platných číslic
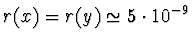 (přesněji
(přesněji
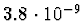 )
)
dostaneme výsledek
x-y = 0.00000369 s přesností na 3 platné číslice
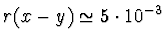 (přesněji
(přesněji
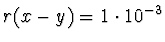 ).
).
Motivace vývoje řady numerických postupů - snaha vyhnout se odečítání
dvou přibližně stejně velkých čísel.
Násobení a dělení nemohou podstatně zvětšit zaokrouhlovací chybu, nejsou
tedy nebezpečné.
Pozn. Dělení číslem 0 je hrubá chyba - nejde o zaokrouhlovací
chybu.
Jiri Limpouch
1999-03-01