Cílem je najít nejkratší cestu, kterou cestující projede všechny uzly a vrátí se zpět do výchozího bodu. Možností je sice konečný počet, ale příliš mnoho na to, abychom je všechny vyzkoušeli. Např. pro 20 mezilehlých uzlů máme
Cílem je nalézt globální minimum
ve velké diskrétní množině, kde může být mnoho lokálních minim.
Příkladem uvedeného typu úlohy je
úloha obchodního cestujícího.
Cílem je najít nejkratší cestu, kterou cestující projede všechny uzly
a vrátí se zpět do výchozího bodu. Možností je sice konečný počet,
ale příliš mnoho na to, abychom je všechny vyzkoušeli. Např. pro
20 mezilehlých uzlů máme
![]() možností.
možností.
Používá se Metropolisův algoritmus (simulované žíhání). Postup má následující kroky:
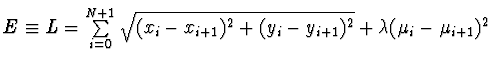 (poslední člen je například pokuta za překročení hranice -
pokud
(poslední člen je například pokuta za překročení hranice -
pokud Elementární změny konfigurací pro úlohu obchodního cestujícího: