

Next: Kombinatorická minimalizace
Up: Hledání extrémů funkce více
Previous: Gauss-Newtonova metoda
Využívá opět explicitní výpočet Hessovy matice.
Jde o kombinaci Gauss-Newtonovy metody s metodou největšího spádu tak,
aby byly eliminovány možné problémy Gauss-Newtonovy metody daleko
od extrému.
Pro Gauss-Newtonovu metodu platí
V Levenberg-Marquardtově metodě nahradíme matici 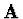 maticí
maticí 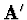
Pokud 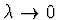 dostáváme Gauss-Newtonovu metodu a pro
dostáváme Gauss-Newtonovu metodu a pro
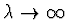 dostáváme malý krok ve směru spádu. Postup
vypadá takto:
dostáváme malý krok ve směru spádu. Postup
vypadá takto:
- Stanovíme vektor
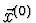 a hodnotu
a hodnotu
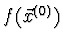 .
.
- Udáme hodnotu
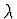 , na příklad
, na příklad
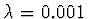 , pro
, pro 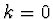 .
.
- Použijeme vztah
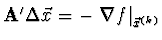 .
.
- Vypočteme hodnotu
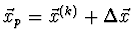 a
a 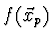 .
.
- Pokud
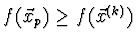 - krok zamítneme
- krok zamítneme
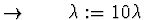 .
.
- je
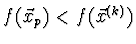 - krok přijmeme
- krok přijmeme
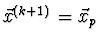 a
a
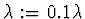 a
a 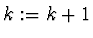 . Dále cyklus opakujeme od třetího kroku.
. Dále cyklus opakujeme od třetího kroku.
Levenberg-Marquardtova metoda se často užívá u nelineární regrese.
Zde minimalizujeme
![$\chi^2 = \sum \limits_{i=1}^N [y_i - y(x_i,
\vec{a})]^2/\sigma_i^2$](img128.gif) vzhledem k
vzhledem k 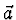 . Pak
. Pak
Část sumy, kde se vyskytují druhé parciální derivace 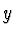 , lze zanedbat,
pro řešení stačí vypočítat matici
, lze zanedbat,
pro řešení stačí vypočítat matici 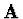 přibližně. Dokonce je
to lepší z hlediska numerické stability.
přibližně. Dokonce je
to lepší z hlediska numerické stability.


Next: Kombinatorická minimalizace
Up: Hledání extrémů funkce více
Previous: Gauss-Newtonova metoda
Jiri Limpouch
2000-04-18
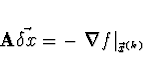
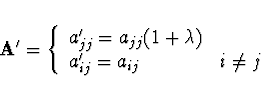
![$\chi^2 = \sum \limits_{i=1}^N [y_i - y(x_i,
\vec{a})]^2/\sigma_i^2$](img128.gif) vzhledem k
vzhledem k ![]() . Pak
. Pak
![\begin{displaymath}
\frac{\partial^2 \chi^2}{\partial a_k \, \partial a_l}=
2 \s...
...a})) \,
\frac{\partial^2 y}{\partial a_k \partial a_l} \right]
\end{displaymath}](img130.gif)