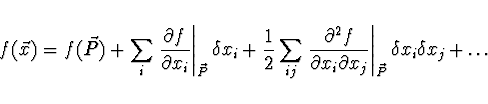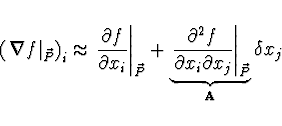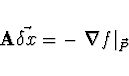

Next: Levenberg-Marquardtova metoda
Up: Hledání extrémů funkce více
Previous: Metoda konjugovaných gradientů
Metoda využívá 2. parciálních derivací, proto je vhodná tam, kde je
umíme snadno spočítat.
Označíme
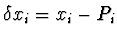 . Nahradíme funkci
. Nahradíme funkci 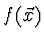 v
okolí bodu
v
okolí bodu 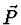 jejím Taylorovým rozvojem
jejím Taylorovým rozvojem
Ponecháme jen členy do 2. řádu včetně a gradient funkce 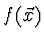 vypočteme
vypočteme
V minimu jsou 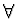 1. parciální derivace nulové a odtud
dostáváme pro
1. parciální derivace nulové a odtud
dostáváme pro
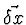 systém lineárních rovnic
systém lineárních rovnic
Je to kvadratická metoda, která může mít problémy daleko od minima.
Jiri Limpouch
2000-04-18
![]() . Nahradíme funkci
. Nahradíme funkci ![]() v
okolí bodu
v
okolí bodu ![]() jejím Taylorovým rozvojem
jejím Taylorovým rozvojem