Newtonův interpolační polynom

Newtonův interpolační polynom je jen jiný zápis Lagrangeova interpolačního polynomu

$$N_n(x) = a_0 + a_1 (x - x_0) + a_2 (x - x_0) (x - x_1) + \dots +$$

$$+ a_n (x - x_0) (x - x_1) \dots (x - x_{n-1})\ \ .$$

Pro vyjádření neznámých koeficientů $a_i$ definujeme poměrné a obyčejné diference.

Poměrné diference
Poměrná diference prvního řádu je definována

$$f(x_i, x_{i+1}) = \frac{y_{i+1} - y_i}{x_{i+1} - x_{i}}\ \ .$$

Poměrnou diferenci $k$-tého řádu definujeme rekurentním vztahem

$$f(x_i, x_{i+1}, \dots, x_{i+k}) = \frac{f(x_{i+1}, \dots, x_{i+k}) - f(x_i, \dots, x_{i+k-1})}{x_{i+k} - x_i} \ \ .$$

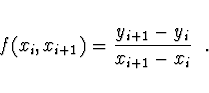
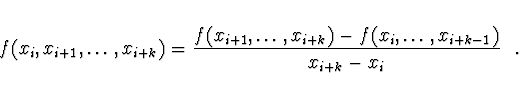
Pozn. Pro poměrnou diferenci druhého řádu platí

$$f(x_i, x_{i+1}, x_{i+2}) = \frac{\frac{y_{i+2} - y_{i+1}}{x_... ...x_{i+1}} - \frac{y_{i+1} - y_i}{x_{i+1} - x_i}}{x_{i+2} - x_i}$$

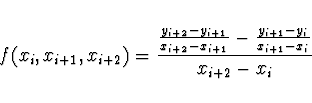
Pozn. Vzorec pro výpočet k-té poměrné diference lze zapsat

$$f(x_i, x_{i+1}, \dots, x_{i+k}) = \sum_{j=0}^k \frac{y_{i+j}}{\prod_{m=0,\ m \not= j}^k (x_{i+j} - x_{i+m})}\ \ .$$

Obyčejné diference
Obyčejná diference 1. řádu je dána

$$\Delta^1 f_i = y_{i+1} - y_i$$

Obyčejná diference $k$-tého řádu je dána

$$\Delta^k f_i = \Delta^{k-1} f_{i+1} - \Delta^{k-1} f_i$$

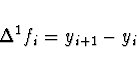
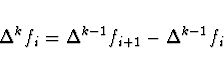
Newtonův interpolační polynom zapíšeme pomocí poměrných diferencí ve tvaru

$$N_n(x) = f(x_0) + (x - x_0) f(x_0, x_1) + \dots +$$

$$+ (x - x_0)(x - x_1) \dots (x - x_{n-1}) f(x_0, x_1, \dots, x_n)$$

Ekvidistantní uzly - Newtonův interpolační polynom má tvar

$$N_n(x) = N_n(x_0 + th) = f(x_0) + \frac{t}{1!} \Delta^1 f_0 + \frac{t(t-1)}{2!} \Delta^2 f_0 + \dots +$$

$$+ \frac{t(t-1) \dots (t - n + 1)}{n!} \Delta^n f_0$$

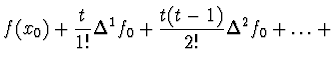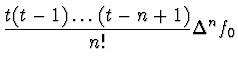Pozn. Newtonovy interpolační polynomy pro uzly předcházející uzlu $x_0$ (Newtonův interpolační polynom vzad)

$$N_n(x) = f(x_0) + (x - x_0) f(x_{-1}, x_0) + \dots + \dots +$$

$$+ (x - x_0) (x - x_{-1}) \dots (x - x_{-n+1}) f(x_{-n}, \dots, x_0)$$