algoritmu (používá se i termín "iterovaná interpolace").
Principem je interpolace pomocí postupně se zvětšujícího počtu uzlů. Postupná přiblížení
Hodnotu ![]() vypočteme přesněji (byť pomaleji)
pomocí Nevillova
vypočteme přesněji (byť pomaleji)
pomocí Nevillova
algoritmu (používá se i termín
"iterovaná interpolace").
Principem je interpolace pomocí postupně se zvětšujícího počtu
uzlů. Postupná přiblížení ![]()
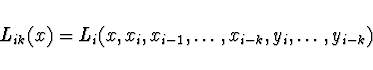
Pro polynomy platí rekurentní vztah
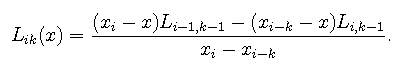
Hodnoty jednotlivých polynomů lze zapsat do tabulky
( Nevillovo schéma)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Lagrangeův interpolační polynom ![]() -tého stupně v bodě
-tého stupně v bodě ![]() je tedy
je tedy
![]() .
.
Odhad chyby aproximace interpolačním polynomem je dán rozdílem
interpolace polynomem řádu ![]() a nejlepší interpolace řádu
a nejlepší interpolace řádu ![]() .
.
Praktická implementace Nevillova algoritmu, zahrnující
odhad chyby využívá vztahů
 |
|||
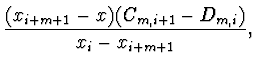 |
V 0-tém kroku zvolíme za aproximaci
![]() hodnotu
v uzlu
hodnotu
v uzlu ![]() nejbližším k x, v každém dalším kroku
nejbližším k x, v každém dalším kroku
![]() , kde
, kde
![]() tak, aby se v každém kroku pokud možno symetricky
rozšířila oblast použitých uzlů,
tak, aby se v každém kroku pokud možno symetricky
rozšířila oblast použitých uzlů,
![]() je odhad chyby
interpolace v daném kroku. Nakonec vypočteme hodnotu interpolačního
polynomu
je odhad chyby
interpolace v daném kroku. Nakonec vypočteme hodnotu interpolačního
polynomu
![]() v bodě
v bodě ![]() a odhad chyby této aproximace
a odhad chyby této aproximace
![]() .
.
Hodnota chyby polynomiální interpolace je dána vztahem
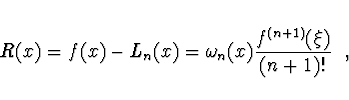
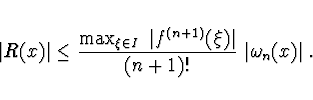
Extrapolace (
![]() ) - chyba rychle roste se
zvětšováním vzdálenosti od krajního uzlu.
) - chyba rychle roste se
zvětšováním vzdálenosti od krajního uzlu.
Vlastnosti interpolace Pro ekvidistantní uzly ![]() má
při vyšších
má
při vyšších ![]() stupních
stupních ![]() interpolační polynom tendenci
obsahovat velké oscilace mezi uzly (pokud sama funkce není polynomem).
Polynomiální interpolace s ekvidistantními uzly vede obvykle
k problematickým výsledkům pro
interpolační polynom tendenci
obsahovat velké oscilace mezi uzly (pokud sama funkce není polynomem).
Polynomiální interpolace s ekvidistantními uzly vede obvykle
k problematickým výsledkům pro ![]() .
.
Konvergence Uvažuji konstantní interval
![]() . Nechť počet
ekvidistantních uzlů
. Nechť počet
ekvidistantních uzlů
![]() (
(
![]() ). Pak konvergence
). Pak konvergence
![]() je zaručena pro funkce analytické
(mající komplexní derivaci) v celé komplexní rovině
s výjimkou
je zaručena pro funkce analytické
(mající komplexní derivaci) v celé komplexní rovině
s výjimkou ![]() . Jinak není zaručena ani bodová konvergence
interpolačního polynomu k funkci.
. Jinak není zaručena ani bodová konvergence
interpolačního polynomu k funkci.
Pozn. Pro neekvidistantní uzly může být situace lepší.
Například pro
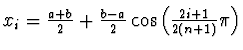 , kde
, kde ![]() ,
konverguje pro
,
konverguje pro
![]() interpolační polynom
k funkci pro
interpolační polynom
k funkci pro ![]() funkce
třídy
funkce
třídy ![]() na intervalu
na intervalu
![]() .
. ![]() aproximace Čebyševovými polynomy
aproximace Čebyševovými polynomy