Implicitní metody jsou vhodné pro lineární diferenciální rovnice,
kde pro výpočet ![]() je nutno řešit systém lineárních rovnic.
Řešit systém nelineárních rovnic je ale obtížné, proto rovnice pro
je nutno řešit systém lineárních rovnic.
Řešit systém nelineárních rovnic je ale obtížné, proto rovnice pro
![]() linearizujeme. Takové metody nazýváme
semiimplicitní.
linearizujeme. Takové metody nazýváme
semiimplicitní.
Linearizujeme implicitní Eulerovu metodu
![]() a dostaneme
a dostaneme
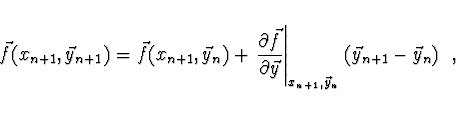
![\begin{displaymath}
\vec{y}_{n+1} = \vec{y}_n
+ h \left[ {\bf I} - \left. h\, \f...
...+1}, \vec{y}_n} \right]^{-1} \cdot \vec{f} (x_{n+1}, y_n)\ \ .
\end{displaymath}](img279.gif)
Pozn. Semiimplicitní metody nejsou A-stabilní, ale dovolují podstatně delší krok než explicitní metody.