![\begin{displaymath}
\int \limits_{x_1}^{x_2} f(x)\, {\rm d}x = h \left[ \frac{1}{2} f_1 +
\frac{1}{2} f_2 \right] + O \left( h^3 f'' \right)
\end{displaymath}](img8.gif)
Lichoběžníkové pravidlo
Vzorec
![\begin{displaymath}
\int \limits_{x_1}^{x_2} f(x)\, {\rm d}x = h \left[ \frac{1}{2} f_1 +
\frac{1}{2} f_2 \right] + O \left( h^3 f'' \right)
\end{displaymath}](img8.gif)
Chybu vzorce můžeme odvodit pomocí rozkladu do Taylorovy řady
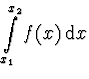 |
![$\displaystyle \int \limits_0^h \left[
f(x_1) + f'(x_1) \tilde{x} + f''(x_1) \frac{\tilde{x}^2}{2} +
\dots \right] d \tilde{x} =$](img11.gif) |
||
![$\displaystyle h [ \frac{1}{2} f_1 +
\frac{1}{2} \underbrace{\left( f_1 + f'(x_1)h + \frac{1}{2}
f''(x_1) h^2 + \dots \right)}_{f_2} ] +$](img12.gif) |
|||
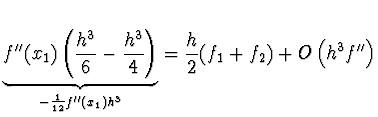 |
Simpsonovo pravidlo
Je to tříbodový vzorec konstruovaný pro polynom druhého stupně,
ale je přesný i pro integraci polynomu třetího stupně
![\begin{displaymath}
\int \limits_{x_1}^{x_3} f(x)\, {\rm d}x = h \left[ \frac{1}...
...} f_2 + \frac{1}{3} f_3 \right] + O \left( h^5 f^{(4)}
\right)
\end{displaymath}](img15.gif)
Simpsonovo 3/8 pravidlo
Je to čtyřbodový vzorec, přesný pro integraci polynomu třetího stupně
![\begin{displaymath}
\int \limits_{x_1}^{x_4} f(x)\, {\rm d}x = h \left[ \frac{3}...
...} f_3 + \frac{3}{8} f_4 \right] +
O \left( h^5 f^{(4)} \right)
\end{displaymath}](img16.gif)