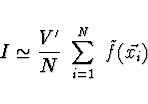Pokud funkci ![]() vypočteme v
vypočteme v ![]() náhodných bodech v integrační oblasti
,
pak
náhodných bodech v integrační oblasti
,
pak
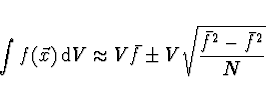
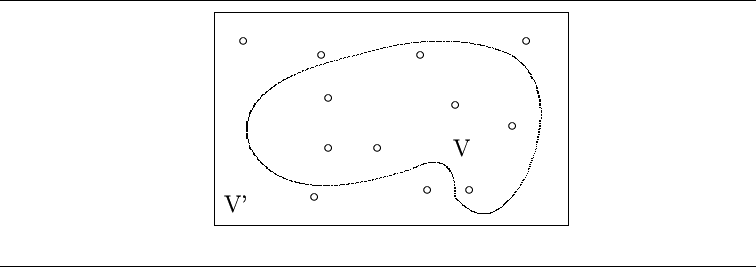
Při výpočtu integrálu metodou Monte Carlo uzavřeme integrační oblast ![]() do co nejmenší oblasti se známým objemem
do co nejmenší oblasti se známým objemem ![]() , ve které
lze snadno generovat náhodné body.
Zavedeme funkci
, ve které
lze snadno generovat náhodné body.
Zavedeme funkci
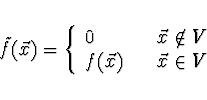
Vygenerujeme ![]() náhodných bodů ve
náhodných bodů ve ![]() a integrál vypočteme
ze vzorce
a integrál vypočteme
ze vzorce