Částečný problém vlastních čísel

Hledáme vlastní číslo největší v absolutní hodnotě.

Zvolíme libovolný vektor $\vec{x}^{(0)}$. A dále počítáme iterace

$$\vec{x}^{(k+1)} = \frac{1}{\varrho_k} {\bf A} \vec{x}^{(k)}\... ...rm příp.} \quad \varrho_k = \Vert {\bf A} \vec{x}^{(k)} \Vert)$$

Pak platí

$$\lim \limits_{k \to \infty} \varrho_k = \lambda_1 \quad \vee \quad \lim \limits_{k \to \infty} \vec{x}^{(k)} = \vec{x}_1$$

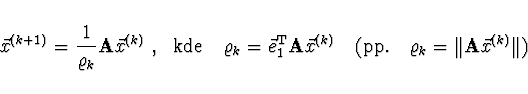
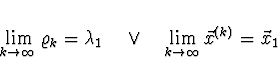
Pokud chceme další vlastní číslo, redukujeme matici na řád $(n-1)$. Je-li vektor $\vec{x}_1 = (u_1, \dots , u_n)^{\rm T}$, platí

$${\bf P} = \left( \begin{array}{cccc} u_1 & 0 & \ldots & 0 \\... ...vec{q}^{\rm T} \\ \vec{0} & {\bf B} \\ \end{array} \right) .$$

dále hledáme maximální vlastní číslo matice ${\bf B}$.

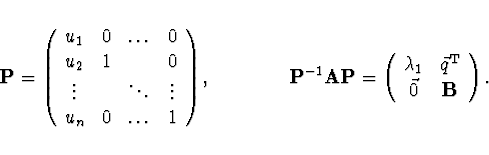
Pozn. Nevýhodou je postupná ztráta přesnosti.

Pozn. Pro výpočet nejmenšího vlastního čísla lze nalézt největší vlastní číslo matice ${\bf A}^{-1}$. Pro hledání vlastního čísla v určité oblasti lze provést posun, neboť $({\bf A} + \mu {\bf I}) \vec{x} = (\lambda + \mu) \vec{x}$.