Příklady nestabilních algoritmů

1. Nestabilní rekurze - ukážeme si na poněkud umělém případu počítání mocnin čísla $\Phi$ zvaného "Zlatý řez"

$$\Phi \equiv \frac{\sqrt{5} - 1}{2} \simeq 0.61803398$$

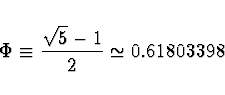
Lehce ukážete, že mocniny $\Phi^n$ splňují jednoduchý rekursní vztah

$$\Phi^{n+1} = \Phi^{n-1} - \Phi^{n}$$

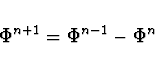
Protože známe $\Phi^0 = 1$ a $\Phi^1 = 0.61803398$ mohli bychom zkusit počítat mocniny odečítáním, což je obvykle rychlejší než násobení.

Obrázek ukazuje, že uvedený postup zcela nepoužitelný, při jednoduché přesnosti dostaneme viditelné chyby výsledky už od n = 16, kdy $\Phi^n \simeq 5.10^{-4}$. Pro n = 20 dostanu poprvé záporný výsledek rekurze, a tedy rekurze už nijak neaproximuje hodnotu mocniny. Nejdříve vzroste relativní chyba (chyba mění znaménko), pak se objeví záporné hodnoty $\Phi^n$ a nakonec začne dokonce růst absolutní hodnoty $\Phi^n$. Nestabilita se projeví i ve dvojité přesnosti, zaokrouhlovací chyba narůstá ale z menší hodnoty a tak by se 1. záporný výsledek rekurze objevil pro n=40.

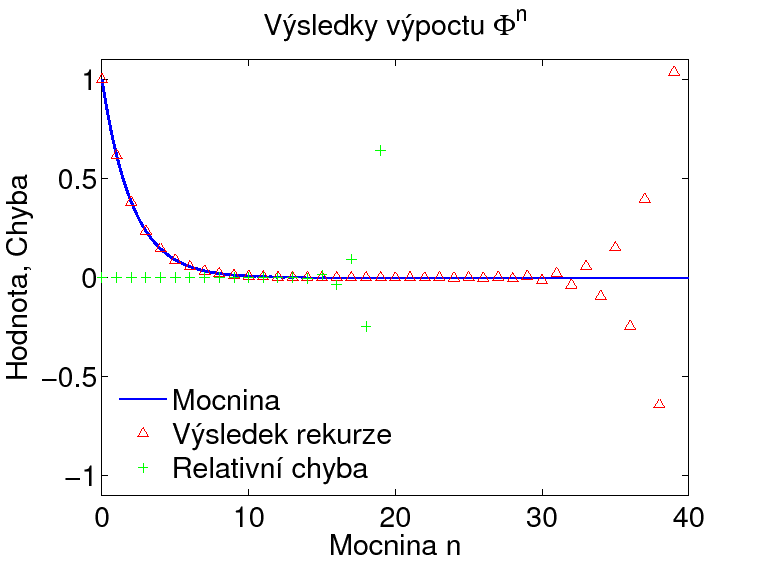
Příčina nestability je v tom, že uvedená rekursní formule má ještě druhé řešení $\Phi_2 = - (\sqrt{5} - 1)/2 < -1 < -\Phi$. Protože rekurzivní relace je lineární, absolutní velikost zaokrouhlovací chyby bude narůstat geometrickou řadou s kvocientem $q = \vert\Phi_2\vert > 1$. Protože navíc řešení klesá, relativní velikost zaokrouhlovací chyby roste geometrickou řadou s kvocientem $q' = \vert\Phi_2\vert/\Phi > 1$. Stejná rekurze by ale mohla být použita pro výpočet mocnin čísla $\Phi_2$. Pro tento výpočet je metoda stabilní a pracovala by uspokojivě.

Uvedený příklad byl umělý, nicméně u mnoha speciálních funkcí (např. Besselovy funkce) se k výpočtu hodnoty funkcí různých řadů používají podobné rekurzivní relace, vždy ovšem tak, aby metoda byla stabilní.

2. Nestabilní metoda pro výpočet obyčejných diferenciálních rovnic

Nechť řešíme obyčejnou diferenciální rovnici 1. řádu

y' = f(x,y)

Na příkladu rovnice y'= - y s počáteční podmínkou y(0) = 1 řešené ve směru růstu proměnné x ukážeme, že dvoukroková metoda 2. řádu

$$y' \simeq \frac{y(x+2h) - y(x)}{2h} = - y(x+h)$$

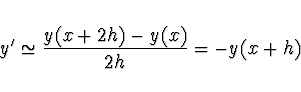
je nestabilní. Jde vlastně o podobnou rekurzi jako výše a pro poměr q = y(x+h)/y(x) existují 2 řešení, $q_1 = -h + \sqrt{1 + h^2}$ je v absolutní hodnotě menší než 1 a odpovídá prvním třem členům Taylorova rozvoje řešení $y = y(0) \cdot \exp(-x)$, druhý kořen $q_2 = -h - \sqrt{1 + h^2}$je v absolutní hodnotě větší než 1 způsobuje nestabilitu algoritmu.

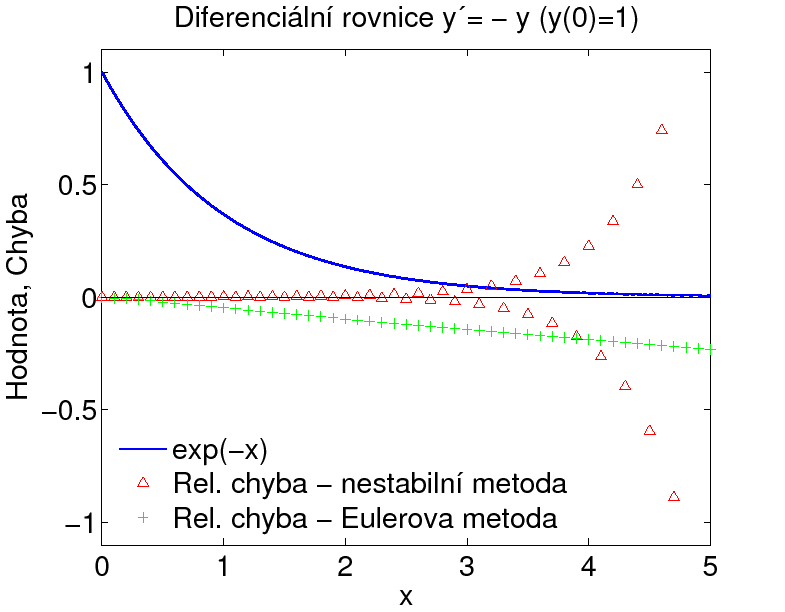
Na následujícím grafu je porovnána celková relativní chyba uvedené nestabilní metody s chybou Eulerovy metody

$$y(x+h) = y(x) + h \cdot y'(x) = y(x) - h\cdot y(x)$$

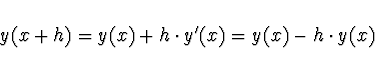
Eulerova metoda se obvykle nepoužívá, neboť jde o metodu 1. řádu s velkou chybou metody, nicméně je pro uvedený případ stabilní.

Obrázek ukazuje, že na začátku řešení je nestabilní metoda vzhledem k relativně malé chybě metody přesnější, ale postupný růst chyby přivede nakonec ke katastrofálním chybám. Katastrofálním chybám nelze zabránit zkracováním kroku, užití dvojité přesnosti katastrofu pouze oddálí. U stabilní metody roste chyba s délkou intervalu nejvýše lineárně a chybu lze zmenšit zkracováním kroku.

3. Nestabilní spline

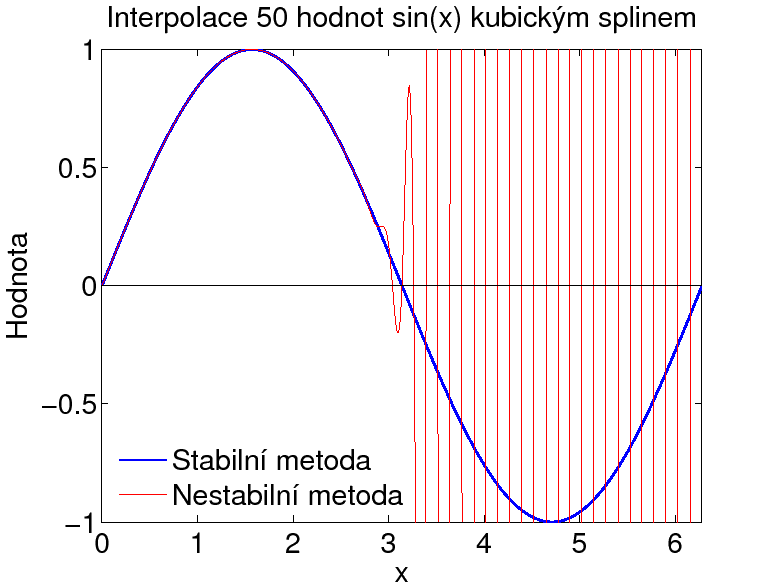
Při interpolaci dat pomocí kubického splinu (lokální interpolace kubickým polynomem se spojitou derivací) je třeba zadat 2 podmínky (např. hodnotu derivace funkce) v obou krajních bodech. Nesprávnou a nestabilní metodu dostaneme, pokud obě podmínky zadáme v 1 z okrajových bodů. Pokud jako 2. podmínku v prvním okrajovém bodu zadáme např. jako 2. derivaci rovnou hodnotě druhé derivace, která vyšla při stabilním postupu, tj. zadaných 1. derivacích v obou okrajových bodech, obě úlohy jsou z matematického hlediska zcela ekvivalentní a v případě počítání s přesnými čísly bych dostal totožný výsledek. Pokud však numericky počítám s konečnou délkou čísel, zaokrouhlovací chyba však při postupném počítání od 1 okraje narůstá a řešení začne mezi zadanými body silně oscilovat.

Na grafu jsou ukázány oscilace chybně počítaného (nestabilního) kubického splinu. Je vidět jen několik prvních extrémů, další jsou v absolutní hodnotě příliš velké (až 10¹³). Při počítání v dvojité přesnosti se viditelné oscilace objeví pro x > 4.