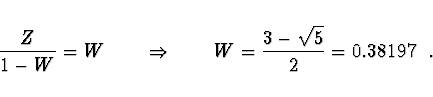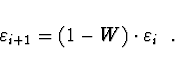K ohraničení minima jsou potřebné 3 body ![]() , ke zúžení
intervalu ohraničujícího kořen potřebujeme 4. bod
, ke zúžení
intervalu ohraničujícího kořen potřebujeme 4. bod ![]() . Označme
. Označme
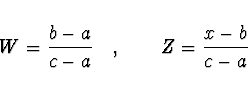

Pokud ![]() , minimum
, minimum
![]() o délce
o délce ![]() z původního, při
z původního, při ![]() minimum
minimum
![]() o délce
o délce ![]() z původního.
Chceme zužovat interval rovnoměrně, tedy
z původního.
Chceme zužovat interval rovnoměrně, tedy
![]() . Dále chceme, aby zužování intervalu mohlo
dále rovnoměrně pokračovat, tedy chceme, aby bod
. Dále chceme, aby zužování intervalu mohlo
dále rovnoměrně pokračovat, tedy chceme, aby bod ![]() dělil
interval
dělil
interval ![]() stejně jako bod
stejně jako bod ![]() dělil interval
dělil interval ![]()