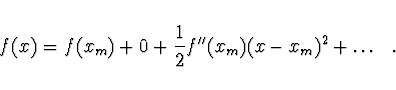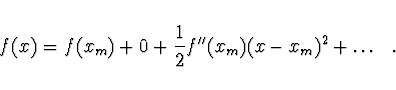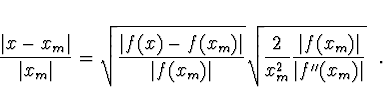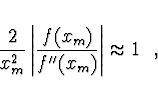

Next: Hledání extrémů funkce jedné
Up: Úvod
Previous: Úvod
Obecně nelze extrémy hledat s tak vysokou přesností jako třeba
řešení rovnic.
Příčinu ukážeme na příkladu minima funkce jedné proměnné.
V okolí minima lze danou funkci dobře aproximovat Taylorovým
rozvojem
Relativní vzdálenost bodu 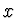 od skutečného minima
od skutečného minima 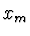 je
je
Jestliže je funkce 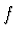 stanovena s relativní přesností
stanovena s relativní přesností 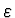 , pak
odchylka nalezeného
, pak
odchylka nalezeného 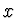 od skutečného minima
od skutečného minima 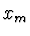 je
je
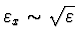 . Pokud lze
považovat
. Pokud lze
považovat
je při jednoduché přesnosti chyba určení extrému
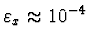 a při dvojnásobné přesnosti je to
a při dvojnásobné přesnosti je to
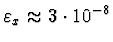 .
.
Jiri Limpouch
2000-04-18