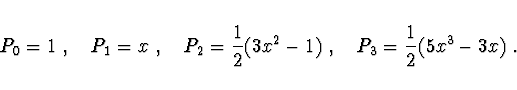

Next: Výpočet funkcí
Up: Aproximace metodou nejmenších čtverců
Previous: Diskrétní aproximace
Skalární součin je pak definován vztahy
Normální rovnice mají tvar
Výběr bázových funkcí
- Ortogonální polynomy
- V případě váhy
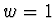 v intervalu
v intervalu
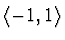 užijeme Legendreovy polynomy,
užijeme Legendreovy polynomy,
Nejnižší Legendreovy polynomy jsou
- Je-li interval
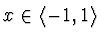 a
váhová funkce
a
váhová funkce
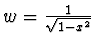 , užijeme
Čebyševovy polynomy
, užijeme
Čebyševovy polynomy 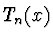 .
.
- Při váhové funkci
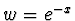 pro všechna
pro všechna
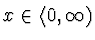 jsou ortogonální Laguerrovy polynomy.
jsou ortogonální Laguerrovy polynomy.
- Při váze
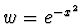 pro všechna
pro všechna
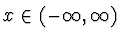 jsou ortogonální Hermiteovy polynomy.
jsou ortogonální Hermiteovy polynomy.
- Trigonometrické funkce - volba trigonometrických
funkcí
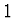 ,
, 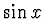 ,
, 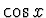 ,
, 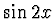 ,
, 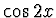 ,
, 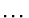 jako
základních funkcí vede k aproximaci Fourierovu řadou. Tyto funkce
jsou ortogonální na
jako
základních funkcí vede k aproximaci Fourierovu řadou. Tyto funkce
jsou ortogonální na
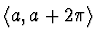 , kde
, kde
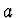 je libovolné. Váhovou funkci pokládáme
je libovolné. Váhovou funkci pokládáme 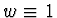 .
.
Jiri Limpouch
2000-03-24
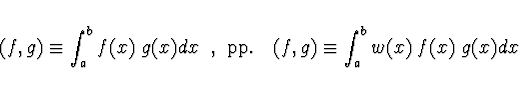
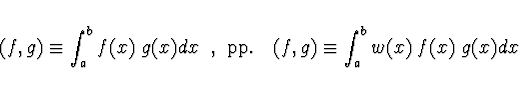
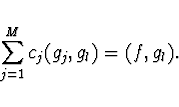
![\begin{displaymath}P_l(x) = \frac{1}{2^l\; l!}\;
\frac{d^l}{dx^l} \left[ x^2 - 1 \right]^l \end{displaymath}](img301.gif)