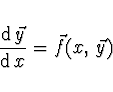
Systém rovnic vektorově
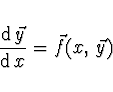
Počáteční podmínky zadávají řešení v bodu ![]() , řešení budeme hledat
postupně v bodech
, řešení budeme hledat
postupně v bodech
![]() . Přibližnou hodnotu
řešení v bodě
. Přibližnou hodnotu
řešení v bodě ![]() nalezneme s pomocí 2 členů Taylorova rozvoje
v bodě
nalezneme s pomocí 2 členů Taylorova rozvoje
v bodě ![]() . Označme
. Označme
![]() . Pak
. Pak
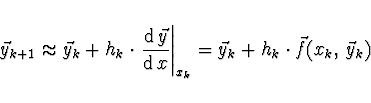
Nejnižší zanedbaný člen určuje odhad chyby k-tého kroku Eulerovy metody
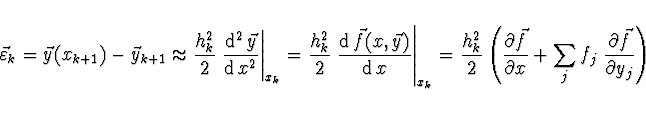
Chyba 1 kroku je tedy úměrná ![]() , počet kroků v daném
intervalu
, počet kroků v daném
intervalu
![]() je
je ![]() a tedy
celková chyba je úměrná
a tedy
celková chyba je úměrná
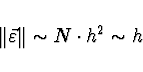
Eulerova metody je metoda 1. řádu (přesnosti). Je tedy
málo přesná, vyžaduje velmi krátký krok, a proto se v praxi
používá jen zřídka.
Pozn. Protože ![]() vzorce pro systém rovnic jsou jen
jednoduchým vektorovým zobecněním vzorců pro 1 rovnici,
budeme dále studovat řešení 1 diferenciální rovnice 1. řádu.
vzorce pro systém rovnic jsou jen
jednoduchým vektorovým zobecněním vzorců pro 1 rovnici,
budeme dále studovat řešení 1 diferenciální rovnice 1. řádu.
Konvergence Eulerovy metody
Nechť je diferenciální rovnice ![]() s počáteční podmínkou
s počáteční podmínkou
![]() . Nechť v oblasti
. Nechť v oblasti
![]() ,
,
![]() je funkce
je funkce ![]() spojitá a ohraničená
spojitá a ohraničená
![]() . Nechť dále
. Nechť dále
![]() a nechť na množině
a nechť na množině ![]()
![]() takové, že platí Lipschitzova podmínka
takové, že platí Lipschitzova podmínka
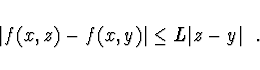
Pozn. Ke splnění Lipshitzovy podmínky stačí, aby funkce ![]() měla
v dané oblasti omezenou parciální derivaci podle
měla
v dané oblasti omezenou parciální derivaci podle ![]() .
.