Metoda konjugovaných směrů

Minimum bychom mohli hledat tak, že bychom je opakovaně hledali postupně v N pevných směrech, tvořících bázi prostoru (např. ve směrech standardní báze). Tento postup může být neefektivní. V případě dlouhých úzkých údolí vede k posloupnosti velmi malých kroků a tedy k velmi pomalé konvergenci k minimu.

$\rightarrow$ Potřeba lepší volby směrů. Chceme volit následující směr tak, abychom neporušili minimum v předchozím $\Rightarrow$ konjugované směry
Pro kvadratickou formu pak získáme minimum po $N$ krocích.

Funkci $f(\vec{x})$ lze v okolí bodu $\vec{P}$ rozvinout do Taylorovy řady ( $\vec{\delta x} = \vec{x} - \vec{P}$)

$$f(\vec{x}) = f(\vec{P}) + \underbrace{\sum \left. \frac{\par... ...\vert _{\vec{P}}}_{{\bf A}_{ij}} \delta x_i \delta x_j + \dots$$

Zde $-\vec{b}$ je gradient v bodě $\vec{P}$ a ${\bf A}_{ij}$ jsou prvky Hessovy matice.

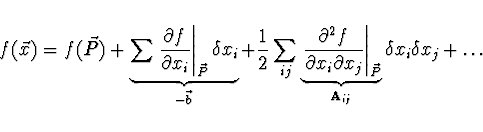
Zachováme-li pouze členy do 2. řádu, pak pro gradient funkce $f(x)$ platí

$$\nabla f(x) = {\bf A} \vec{\delta x} - \vec{b} \qquad {\rm a} \qquad \delta (\nabla f) = {\bf A} (\vec{\delta x})\ \ .$$

Když minimalizace ve směru $\vec{v}$ nemá poškodit minimum ve směru $\vec{u}$, musí platit

$$\vec{u}^T \delta (\nabla f) = 0 \quad \Rightarrow \quad \vec{u}^T {\bf A} \vec{v} = 0$$

Vektory $\vec{u}$ a $\vec{v}$ určují konjugované směry.

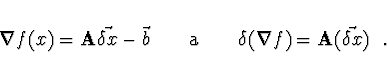
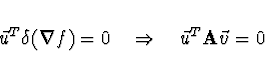
Následující metodu konjugovaných směrů navrhl roku 1964 Powell. V prvním kroku volíme směry $\vec{u}_i = \vec{e}_i$, kde $i = 1, \dots, N$. Jako další směr volíme $\vec{p}_N = \vec{P}_N - \vec{P}_0$, tedy směr ke kterému vedlo N minimalizací ve směru. Z původní báze směrů 1. směr vynecháme.

Tato metoda je kvadraticky konvergentní, pro kvadratickou formu minimalizace ve směru $\vec{p}_N$ najde minimum.

Navržená metoda může ovšem vést ke vzniku lineární závislosti souboru $N$ vektorů směrů minimalizace.
Jsou následující možnosti odstranění tohoto problému

1. Reinstalujeme směry $\vec{u}_i$ po každém $N$ i $N+1$ iteracích.
2. Brentova metoda - dokalkuluje směry sofistikovanými postupy,
3. Vynecháme směr, kde došlo k maximálnímu poklesu. Ten dal maximální příspěvek k $P_N - P_0 \ \Rightarrow$ lineární nezávislost směrů se zachovává, metoda ale ztrácí kvadratickou konvergenci.