Převedení ukážeme na příkladu
Zavedeme pomocné proměnné ![]() ,
, ![]() ,
, ![]() a tak podmínky
s nerovnostmi převedeme na rovnost
a tak podmínky
s nerovnostmi převedeme na rovnost
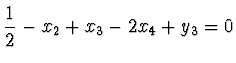 |
|||
Sestavíme tabulku pro omezenou normální formu
| |
|
|
|
|
||
|
|
0 | 1 | 1 | 3 | |
0 |
|
|
740 | -1 | 0 | -2 | 0 | 0 |
|
|
0 | 0 | -2 | 0 | 7 | 0 |
|
|
|
0 | -1 | 1 | -2 | 1 |
|
|
9 | -1 | -1 | -1 | -1 | 0 |
|
|
|
1 | 2 | 0 | 3 | -1 |
Vybereme hlavní element na příklad ze sloupce ![]() , na třetím řádku
je
, na třetím řádku
je ![]() , na čtvrtém
, na čtvrtém ![]() , ale na druhém
, ale na druhém
![]() . Z druhého řádku máme
. Z druhého řádku máme
![]() .
Kdybychom vzali hlavní prvek ze 3. řádku, bylo
by po úpravě na 2. řádku
.
Kdybychom vzali hlavní prvek ze 3. řádku, bylo
by po úpravě na 2. řádku
![]() .
To je ovšem chybně, konstanta nesmí být záporná (
.
To je ovšem chybně, konstanta nesmí být záporná (![]() ).
Po úpravě má tabulka tvar
).
Po úpravě má tabulka tvar
| |
|
|
|
|
||
|
|
0 | 1 | |
3 | 3 | 0 |
|
|
740 | -1 | 0 | -2 | 0 | 0 |
|
|
0 | 0 | |
0 | |
0 |
|
|
|
0 | |
1 | |
1 |
|
|
9 | -1 | |
-1 | |
0 |
|
|
|
1 | -1 | 0 | 10 | -1 |
Hlavní sloupec je pod ![]() , hlavní element (
, hlavní element (![]() ) je v
řádku u
) je v
řádku u ![]() , odtud vyjádříme
, odtud vyjádříme
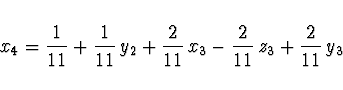
| |
|
|
|
|
||
|
|
|
1 | |
|
|
|
|
|
740 | -1 | 0 | -2 | 0 | 0 |
|
|
|
0 | |
|
|
|
|
|
|
0 | |
|
|
|
|
|
|
-1 | |
|
|
|
|
|
|
1 | |
|
|
|
Nyní z řádku u ![]() dostaneme
dostaneme
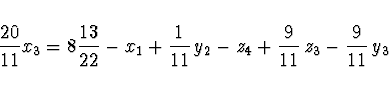
| |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 | 0 | 0 | -1 | -1 | 0 |
Jakmile dostaneme všechna ![]() na pravou stranu,
můžeme je vynechat, pomocná účinková funkce
na pravou stranu,
můžeme je vynechat, pomocná účinková funkce ![]() je minimalizována a
vynecháme ji. Úloha je převedena na omezenou normální formu.
je minimalizována a
vynecháme ji. Úloha je převedena na omezenou normální formu.
V našem případě jsou už u ![]() skutečných pravostranných
proměnných (
skutečných pravostranných
proměnných (![]() ,
, ![]() ,
, ![]() ) koeficienty u účinkové funkce
) koeficienty u účinkové funkce ![]() záporné a úloha je tedy vyřešena
záporné a úloha je tedy vyřešena
 |
|||
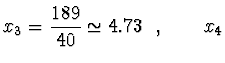 |
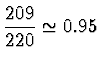 |
||
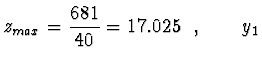 |
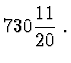 |
Degenerovaný možný vektor - stejně velké
omezení ve více řádcích ![]() více možných hlavních prvků.
Potom se rozhodujeme při výběru rozhodujeme podle dalších
sloupců.
více možných hlavních prvků.
Potom se rozhodujeme při výběru rozhodujeme podle dalších
sloupců.